What is an Algorithm?

It is a set of instructions given to the computer to solve a problem.

Types of complexity:

1. Time complexity

It describes the amount of time a computer takes to run an algorithm.

2. Space complexity

It describes the amount of memory space required to solve an instance of a problem.

---

TIME COMPLEXITY

Let's check an example:

print("Coding")

The Time complexity of the above line of code is 1 (one).

for i in range(0,10):
    print("Coding")

The Time complexity of the above code is 10 (The upper bound of the range).

Time Complexity Analysis:

There are two methods for Time Complexity Analysis:

1. Experimental Analysis

2. Theoretical Analysis

Experimental Analysis:

Let's see an example:

So as you run the code the time keeps changing :

As it depends on various factors such as the OS of a user etc time keeps changing and thus experimental analysis is not the preferred method to analyze time complexity.

Theoretical Analysis

Here the Big O notation comes into the picture.

BIG 'O' NOTATION:

It describes the runtime of an algorithm in terms of how quickly it grows relative to input.

Types of Big 'O' Notation:

1. Best case

2. Average case

3. Worst case

Rules to calculate time complexity with Big 'O' notation

1. Consider only the highest degree.

2. Drop all the constants

    print("Hi");                //Time=C1
    print("Hello");             //Time=C2
    print("Hey");               //Time=C3
   

   $$Tc=C1+C2+C3 $$

   $$Tc=O(c)$$

   As

   $$C1+C2+C3=C$$

   Drop the constants

   $$Tc=O(1)$$

Big 'o' time complexity graph:

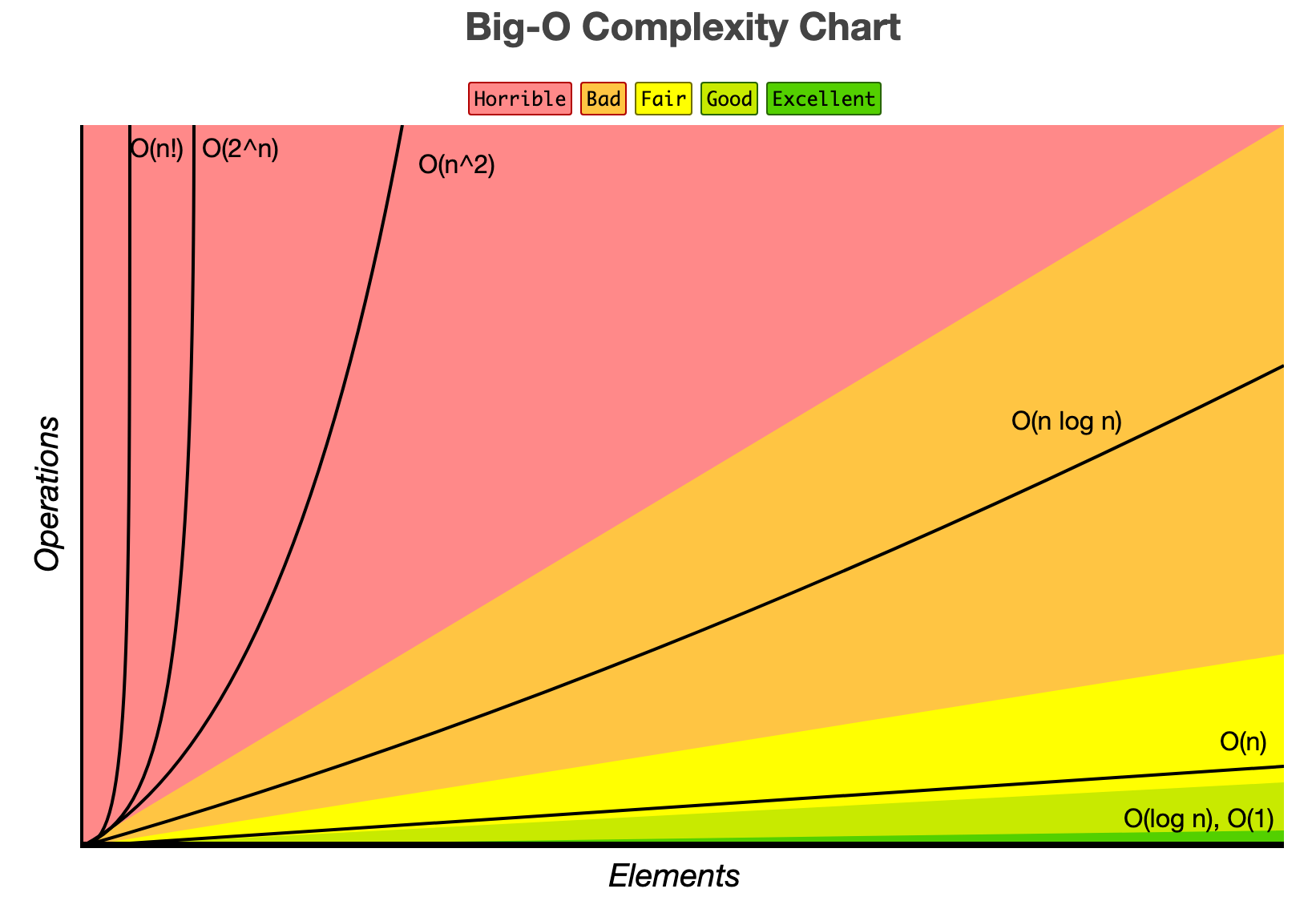
Some Imp Time complexities:

$$O(1)<O(log n)<O(√n)<O(n)<O(nlogn)<0(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)$$